Hipérbola: La ecuación de una hipérbola

Te habrás dado cuenta de que según la posición de sus vértices, focos y eje transversal, una hipérbola puede ser horizontal o vertical. Para obtener su ecuación ordinaria (también se le llama ecuación canónica) es necesario partir de la definición de hipérbola: el conjunto de puntos cuya diferencia de distancias a los focos es constante:

Ello implica calcular las distancias , , obtener la diferencia y simplificar mediante trabajo algebraico, llegando finalmente a las siguientes ecuaciones:

Para una hipérbola horizontal:

Para una hipérbola vertical:

Donde:
a= longitud del semieje transverso
b= longitud del semieje conjugado
(h, k): coordenadas del centro de la hipérbola

Para seguir paso a paso el desarrollo matemático que lleva a estas ecuaciones, oprime aquí.

¿Te fijas? Estas ecuaciones también son muy parecidas a las de las elipses horizontales y verticales. ¿Puedes distinguir las diferencias?

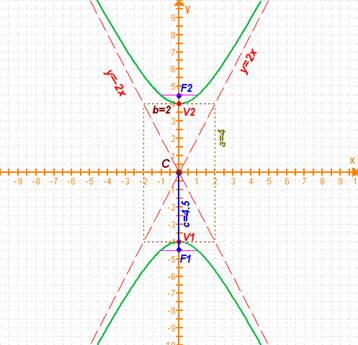
Obtengamos la ecuación de la hipérbola de nuestro ejemplo:

Para empezar la gráfica no deja dudas respecto al tipo de hipérbola: es vertical. En cuanto a los parámetros que necesitamos, puedes verificar en la gráfica que a=4,b=2 y C(0,0), así que sustituiremos estos valores en:

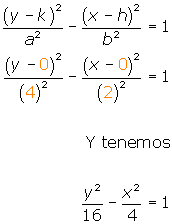Realizamos la suma de fracciones obteniendo un denominador común:

Multiplicamos ambos lados por (64) para que los coeficientes sean enteros:

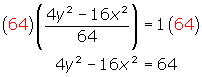Ordenamos la ecuación:

Recuerda que en las ecuaciones los coeficientes nos dan toda la información que necesitamos para construir la gráfica, así que aprovecha este ejemplo para observar y contestarte: ¿qué relación hay entre los coeficientes de esta ecuación y los elementos de la gráfica?