| |
|
| |
|
| |
Hipérbola: Esta es la solución |
| |
|
|
Resolvamos este reto juntos: |
| |
|
| |

|
| |
|
| |
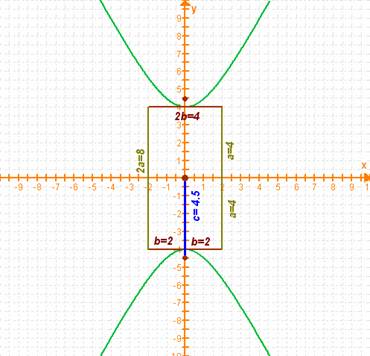
El eje transverso mide lo mismo que el lado mayor del rectángulo. Si cuentas en la gráfica verás que su longitud es de 8 unidades. Como nos piden el semieje transverso a, lo dividimos entre dos y tenemos a=4. |
| |
|
| |
|
| |
|
| |
El eje conjugado y el lado corto del rectángulo miden lo mismo: 4 unidades, así que el semieje mide b=2. Podemos ver que el valor de c no es un entero así que, para no tener que usar una aproximación visual, podemos aprovechar la relación c2=a2+b2. Por ello: |
| |
|
| |
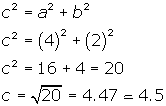
|
| |
|
| |
En cuanto a la longitud del lado recto, tenemos que: |
| |
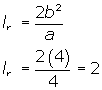
|
| |
Podemos calcular la excentricidad así: |
| |
|
| |
|
| |
Ahora trabajemos con las coordenadas de los puntos. Podemos distinguir el centro, entre otras características, por ser el punto donde se cruzan las asíntotas. En este caso, el centro está en C(0,0). |
| |
|
| |
|
| |
|
| |
En cuanto a los vértices, que son los puntos donde cada una de las ramas de la hipérbola cambian su curvatura, puedes ver que se encuentran en V1 (0,-4) y V2(0,4). Puedes verificar entonces el valor de a, que es la distancia entre el centro y el vértice. Los focos se encuentran en F1(0,-4.5) y F2 (0,4.5). Puedes verificarlo si recuerdas que la distancia c vale precisamente 4.5. |
| |
|
| |
Para obtener las ecuaciones de las asíntotas necesitamos dos parámetros, la pendiente y la ordenada al origen. Como recuerdas, para determinar la pendiente necesitamos determinar el desplazamiento horizontal y vertical entre dos puntos de la recta. Por ejemplo para llegar de (-2,4) a (-1,2) nos desplazamos 2 unidades hacia abajo (lo representamos así: 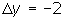 ) y una unidad a la derecha ( ) y una unidad a la derecha (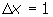 ), por lo que: ), por lo que: |
| |
|
| |
|
| |
|
| |
En este caso, la ordenada al origen es b1=0 porque para esta recta, las coordenadas del punto de intersección con el eje y son (0,0). Así , la asíntota 1 tiene la siguiente ecuación: |
| |
|
| |
|
| |
|
| |
Análogamente para la asíntota 2 puedes verificar que su pendiente es m2=2 y su ordenada al origen es b2=0, por lo que la ecuación de esta recta es y=2x. Nuestra gráfica con todos sus elementos se ve así: |
| |
|
| |
|
| |
|
| |
| |
|
|
|
|
|
 |
 |
|
|
|
|
| |
|
|
7/11 |
|
|
|
|
|
|
|
|
|